How to Better Remember Spring and Resistance Equivalent Constant Formulas

Problem

This year I've been using Anki to memorize useful Physics formulas. While theoretically I should be able to derive everything from first principles on the spot every time, the practicalities saves me time and mental energy when working on problems.

But I've had trouble memorizing formulas for finding equivalent proportional constants. It's easy to get confused between the formulas for each law since they look very similar. As an example let's compare springs in parallel to resistors in parallel.

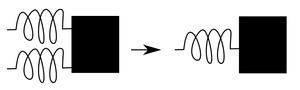
If two springs are pulling in parallel like in the figure, we can simplify to one spring by describing the force exerted by one spring as \(F_1 = k_1 \Delta{x}\), the force from the other as \(F_2 = k_2 \Delta{x}\), and the force exerted by our equivalent spring as \(F_1 + F_2 = k_\text{eq} \Delta{x}\). Thus \(k_\text{eq} = k_1 + k_2\).

But the equivalent resistance for Ohm's Law resistors which are also in parallel, and whose diagrams are pretty visually similar, have a completely different mathematical relationship!!

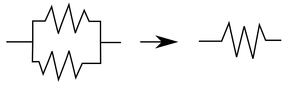
We'll call \(I_1\) the current running through the top resistor, and \(I_2\) the bottom. We know that the voltage is equal across both endpoints of each resistor, so \(\Delta{V} = I_1 R_1\), \(\Delta{V} = I_2 R_2\). Our simplified resistor has resistance \(R_\text{eq}\), and thus \(R_\text{eq} \sum I_i = \Delta{V}\). Thus \(\frac{1}{R_\text{eq} }  = \frac{1}{R_1} + \frac{1}{R_2}\).

It was frustrating to remember the difference, so I made a general formula to cover all similar situations where I have to memorize equivalent proportional coefficients for things in linear proportionality.

Solution

General Technique

A linear proportional relationship between two quantities, \(Y\) and \(X\), can be expressed as \(Y = XP\) where \(P\) is some constant.

Case 1: \(Y_i\) Add Together and \(X\) is Constant

In one set of equivalent constant theorems, \(X\) remains constant but the \(Y_i\) add together. In other words

\[ \sum Y_i = Y \]

We know from the linear relationship that our big \(Y\) is itself related to the quantity \(X\) by the "equivalent" proportionality constant that we're looking for: \(P_\text{eq}\).

\[ \sum XP_i = XP_\text{eq} \]

\(X\) is constant, so we can divide through all the terms of the sum by \(X\).
\[
\sum P_i = P_\text{eq}
\]

Thus in situations like Case 1, we can find the equivalent proportionality constant by adding together the proportionality constants.

Case 2: \(Y\) is Constant and \(X_i\) Add Together

We can also express our linear proportional relationship as \(\frac{Y}{P} = X\). From the premise of Case 2, we can say
\[
\sum X_i = X
\]
Using similar logic from Case 1, we can reduce that equation to finding our equivalent proportionality constant.
\[
\sum \frac{Y}{P_i} = \frac{Y}{P_\text{eq} }
\]
\[
\sum \frac{1}{P_i} = \frac{1}{P_\text{eq} }
\]

Now that we have our formulas for both cases, let's apply it to spring coefficients and electrical resistances.

Examples

Also, for some visuals I'd recommend visiting Wikipedia (Springs: https://en.wikipedia.org/wiki/Series_and_parallel_springs)  (Resistors: https://en.wikipedia.org/wiki/Resistor#Series)

Equivalent Constants for Springs

First, we check that Hooke's Law is indeed a linearly proportional relationship: force is linearly proportional to displacement \(F = k \Delta{x}\). 

Now let's tackle springs in parallel and series.

Springs in Parallel

We can simplify this system into just one spring attached to the block. Each spring experiences the same displacement; in other words \(\Delta{x}\) is constant. (We assume this block is not experiencing net torque and rotation from one of the springs pulling harder.) We also say that the sum of each spring's force is equal to the force the simplified spring contributes, i.e. \(\sum F_i = F\).

This should be ringing bells, this situation matches the conditions for applying Case 1 of my general technique! The \(Y_i\) add together but \(X\) is constant.

Thus the equivalent Hooke's Law constant must be the sum of the constants of the smaller springs, i.e. \(\sum k_i = k_\text{eq}\).

Springs in Series

Now let's consider the case where the springs are attached in series. We say that all the forces from each spring are equal, i.e. \(F\) is constant. (If the force were unequal, then one spring would pull harder on another, stretching it, and creating an oscillation effect. So we're assuming for simplicity's sake that the forces are constant.) We also say that the displacement of each spring adds up to the total displacement of the big equivalent spring, i.e. \(\sum \Delta x_i = \Delta x\). This fits Case 2! The \(Y\) is constant but the \(X_i\) add together. So we can quickly conclude that the equivalent spring constant is

\[
\sum \frac{1}{k_i} = \frac{1}{k_\text{eq}}
\]

Equivalent Electric Resistances

Consider doing the derivation for the following yourself before seeing my solution, since making an independent attempt at this \(Y=XP\) thing will help your understanding a lot.

First, we check to make sure the physical law here is indeed a linear proportionality: \(\Delta{V}=IR\).

Resistors in Parallel

Voltage differences across resistors in parallel are equal, but currents running across each resistor may be different. Thus this is an instance of Case 2, the \(Y\) is constant but the \(X_i\) add together, and so we can jump immediately to the formula:

\[
\frac{1}{R_\text{eq} } = \frac{1}{\sum R_i}
\]

Resistors in Series

Resistors in series have different voltage differences across them, as each resistor reduces the voltage. But there is only one current running across all the resistors. Thus this is an instance of Case 1, The \(Y_i\) add together but \(X\) is constant, and so our equivalent proportionality constant must be

\[
R_\text{eq} = \sum R_i
\]